En esta sesión hemos comenzado con el tema 2, tratando aspectos básicos de trigonometría y vectores.
En este vídeo revisamos los conceptos básicos sobre triángulos rectángulos que usaremos a lo largo del curso.
[BMC-001] Conceptos básicos de trigonometría. Triángulos rectángulos. (07:24)
Vídeo
este es un problema de aplicación directa de las fórmulas básicas de la trigonometría.
[BMC-002] 4. (12:15)
En un triángulo rectángulo los catetos miden 5 y 7 m respectivamente. Calcular el valor de los dos ángulos agudos del mismo. Resp.: ? = 35.55º; ?= 54.55º
Vídeo
Este problema es de aplicación directa de las definiciones trigonométricas. Lo resolvemos de dos maneras distintas: muchas veces no hay un camino único para resolver un problema, y un camino no tiene porqué ser necesariamente mejor o peor.
[BMC-003] 3. (04:26)
En un triángulo rectángulo el ángulo menor mide 30º y la hipotenusa 6 m. Calcula el valor de ambos catetos. Resp.: 5.20 m y 3.0 m
Vídeo
En este vídeo vemos lo básico del sistema de coordenadas rectangulares o cartesiano, vamos, el de toda la vida.
[VID-23796] Sistema de coordenadas rectangulares o cartesianas. (07:16)
Vídeo
En este vídeo introducimos el concepto de las magnitudes vectoriales. Vemos como obtener las componentes de un vector mediante las coordenadas de sus extremos, y vemos que estas son independientes del origen de coordenadas que tomemos.
[VID-23797] Vectores. Generalidades. (16:27)
Vídeo
En este ejercicio partimos de la definición de un vector por su módulo y su dirección y obtenemos sus componentes cartesianas. El módulo y la dirección de un vector constituyen lo que se llaman las coordenadas polares, y son otra manera de expresar el vector alternativa a las cartesianas. Es como una mesa, si la nombras en español es "mesa", mientras que en inglés es "table", pero sigue siendo la misma mesa. Aunque digas en alemán "kartofell".
[BMC-006] 5. (07:16)
La fuerza neta que actúa durante la batida de un saltador de longitud es de 1500 N. Si dicha fuerza actúa con un ángulo de 70º, como se indica en la figura. ¿Cuál sería la componente vertical de dicha fuerza?
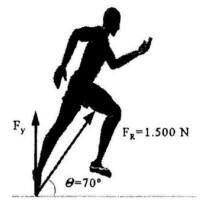
Vídeo
En este ejercicio obtenemos el módulo y la orientación de un vector definido por las coordenadas de sus extremos. Nos apoyamos, como siempre que podemos, en la representación gráfica. También lo resolvemos por un enfoque más de fórmulas.
[VID-23798] 9. (07:18)
¿Cuál es la magnitud del vector posición definido en sus extremos por las coordenadas de los puntos A(2,1) m y B(5,7) m? Resp.: r = 6.7 m
